【题解】P3147 [USACO16OPEN]262144 P

发表于 分类于 阅读次数： Valine：

题目链接（洛谷）

题目大意

有一种游戏，游戏一开始有n个正整数，\((2\le n\le 2^{18} )\)，范围在\([1,40]\)。在一步中，可以选相邻的两个相同的数，然后合并成一个比原来的大一的数（例如两个\(7\)合并成一个\(8\)），目标是使得最大的数最大，请求最大值。

分析

设\(dp(i,j)\)为左端点为\(j\)，合并出数字\(i\)时右端点的位置。通过下面数轴可以得出转移方程：

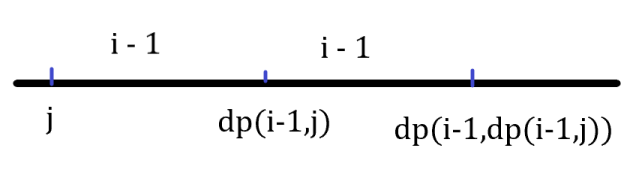\[ dp(i,j)=dp(i-1,dp(i-1,j)) \] 关于\(i\)的枚举范围，因为\(n\le 2^{18}\)，所以\(i\le 40+18=58\)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<bits/stdc++.h>
using namespace std;
int dp[60][270000];
int n,a[270000];
int ans;
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        dp[a[i]][i]=i+1;
    }
    for(int i=2;i<=58;i++){
        for(int j=1;j<=n;j++){
            if(!dp[i][j]) dp[i][j]=dp[i-1][dp[i-1][j]];
            if(dp[i][j]) ans=i;
        }
    }
    cout<<ans;
    return 0;
}