赵嘉熠的博客

随笔一篇

题目链接（正睿）

题目大意

有$2^n$个人玩剪掉石头布，每次第$1$个人和第$2$个，第$3$个和第$4$个……会决出谁是胜者，然后晋级下一轮变成第$1,2,3…$个人。经过$n$轮后最后会决出一个胜者。

这$2^n$个人每次出拳都固定，其中有$r$个石头，$p$个布，$s$个剪刀。给出一组出拳方案，用R来表示石头，P来表示布，S来表示剪刀。使得任意一轮比赛都不存在出拳相同的人，且字典序最小。

$n\le 15$

题目链接（洛谷）

题目大意

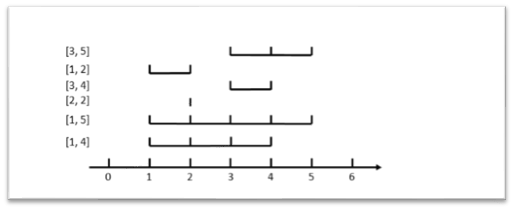
在数轴上有$n$个闭区间从$1$至$n$编号，第$i$个闭区间为$[l_i,r_i]$。现在要从中选出$m$个区间，使得这$m$个区间共同包含至少一个位置。换句话说，就是使得存在一个$x$，对于每个被选中的区间$[l_i,r_i]$，都有$l_i \le x \le r_i$。

对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。

区间 $[l_i,r_i ]$的长度定义为$(r_i-l_i)$，即等于它的右端点的值减去左端点的值。求所有合法方案中最小的花费。如果不存在合法的方案，输出$−1$。

$1 \le m \le n,~1 \le n \le 5 \times 10^5,~1 \le m \le 2\times 10^5,~0\le l_i \le r_i \le 10^9$

题目链接（洛谷）

题目大意

给定常数$k$。对于一个长度为$n$的排列$a$，定义

$
f(a)={\max{1 \le i \le k} {a_i},\max{2 \le i \le k+1} {ai},\cdots,\max{n-k+1 \le i \le n} {a_i}}
$

对于一个长度为$n$的序列$a$，定义其权值$w(a)$为$a$中不同的数的个数。

求对于长度为$n$的排列$p$，它们的$w(f(p))$之和。

$1\le k \le n \le 5\times 10^5$

题目链接（洛谷）

题目大意

有$n(n\le 10000)$种不同的邮票，皮皮想收集所有种类的邮票。唯一的收集方法是购买，每次只能买一张，并且买到的邮票究竟是$n$种邮票中的哪一种是等概率的，概率均为$\frac{1}{n}$。购买第$k$次邮票需要支付$k$元钱。

求得到所有种类的邮票需要花费的钱数目的期望。

题目链接（洛谷）

题目大意

给定一个长度不超过$105$的字符串（小写英文字母），和不超过
$50000$个操作。

每个操作$L,R,K$表示给区间$[L,R]$的字符串排序，$K=1$为升序， $K=0$为降序。

最后输出最终的字符串。

题目链接（洛谷）

题目大意

考虑排好序的$N(1\le N \le 31)$位二进制数，且包含所有长度为$N$且这个二进制数中$1$的个数小于等于$L(l\le N)$的数。

现在输出满足长度为$N$，且$1$的个数小于等于$L$的第$k$小的那个二进制数。

比赛链接（BNDSOJ）

题目链接（洛谷）

题目大意

给出三类函数，分别可以实现下面三种功能：

1. 单点加；

2. 全局乘；

3. 依次执行若干次函数调用，保证不会出现递归。

给出$n$个数据的出初始值，并给出$m$个函数调用，求最后的数据。

$1\le n \le 10^5$

题目链接（洛谷）

题目大意

给出$n(1\le n \le 5\times 10^5)$个点和$n-1$条连着它们的路径，每一条道路都连接某两个点，且通过这些道路可以走遍所有的点。

有$m(1 \le m \le 10^5)$组人分散在这些点上，每组有三个人。给出每组中三人的初始位置。每组确定一个位置使每组内三人到这个点的距离和最小，输出这个距离和。